Plot phase portrait with matlab and simulink
Table of Contents
Table of Contents
Have you ever struggled with drawing a phase portrait by hand? It can be a challenging task, but with the right techniques, it doesn’t have to be intimidating. In this blog post, we will go over everything you need to know to draw a phase portrait by hand.
When it comes to drawing a phase portrait by hand, there are several pain points that can make it difficult. For example, understanding the concept of phase space, knowing how to find critical points, and determining the behavior of solutions near those points. These are all important aspects to consider, and without a clear understanding of them, it can be hard to draw an accurate phase portrait.
The first step towards drawing a phase portrait by hand is to have a clear understanding of what a phase portrait is. A phase portrait is a graphical representation of the behavior of solutions to a system of differential equations. It provides insight into the long-term behavior of the system and can help you identify stable and unstable critical points.
To draw a phase portrait by hand, you need to follow these steps:
Step 1: Identify critical points
The first step is to identify the critical points of the system. Critical points are the points where the solution is either zero or undefined. These points are important because they help determine the behavior of the solutions near them.
For example, consider the system of differential equations:
The critical points of this system are (0,0) and (1,1). To find these points, you need to set both differential equations equal to zero and solve for x and y.
Step 2: Determine the behavior of solutions near critical points
Once you have identified the critical points, you need to determine the behavior of solutions near them. This can be done by analyzing the eigenvalues of the Jacobian matrix evaluated at each critical point.
The Jacobian matrix is a matrix of partial derivatives that describes the behavior of the system near a given point. The eigenvalues of this matrix tell you whether the critical point is stable, unstable, or a saddle point.
Step 3: Sketch the phase portrait
Now that you have identified the critical points and determined their behavior, you can start sketching the phase portrait. To do this, draw a small arrow at each point in the direction that the solution is moving. The direction of the arrow should be based on the behavior of the nearby solutions.
Conclusion
Learning how to draw a phase portrait by hand can take some time and effort, but with practice, it is a skill that anyone can master. By following the steps outlined in this article, you can start sketching accurate phase portraits in no time.
Personal Experience: Understanding the Importance of Critical Points
When I first started learning about drawing phase portraits by hand, I struggled to understand the importance of critical points. It wasn’t until I started working through several examples that I realized just how critical they are in determining the behavior of the system.
For example, in the system of differential equations:
There are three critical points: (0,0), (0,1), and (1,0). At each of these points, the behavior of the system is different.
The critical point (0,0) is a saddle point, which means that there are stable and unstable solutions near it. The critical point (0,1) is a stable node, which means that all nearby solutions converge to it. Finally, the critical point (1,0) is an unstable node, which means that all nearby solutions move away from it.
Understanding the behavior of solutions near critical points is essential in drawing an accurate phase portrait. Without this understanding, your portrait may not accurately reflect the true behavior of the system.
Identifying Stable and Unstable Trajectories
Another important aspect of drawing a phase portrait is identifying stable and unstable trajectories.
Stable trajectories are solutions that move towards a critical point and stay there. Unstable trajectories, on the other hand, move away from the critical point and never return.
By analyzing the eigenvalues of the Jacobian matrix at each critical point, you can determine whether nearby trajectories are stable or unstable. This information can be used to accurately sketch the phase portrait.
Practice Example
Consider the system of differential equations:
The critical point of this system is (0,0). To analyze its behavior, we evaluate the Jacobian matrix at this point:
The eigenvalues of this matrix are both negative, which means that the critical point is a stable node. All nearby trajectories will converge to it.
Question and Answer
Q: What is a phase portrait?
A: A phase portrait is a graphical representation of the behavior of solutions to a system of differential equations.
Q: Why are critical points important in drawing a phase portrait?
A: Critical points are important because they help determine the behavior of solutions near them.
Q: How do you determine the behavior of solutions near critical points?
A: The behavior of solutions near critical points can be determined by analyzing the eigenvalues of the Jacobian matrix evaluated at each critical point.
Q: What are stable and unstable trajectories?
A: Stable trajectories are solutions that move towards a critical point and stay there. Unstable trajectories, on the other hand, move away from the critical point and never return.
Conclusion of how to draw phase portrait by hand
Drawing a phase portrait by hand can seem like a daunting task, but by following the steps outlined in this article, you can successfully draw an accurate portrait. Understanding the importance of critical points and being able to analyze the behavior of solutions near them is key in drawing an accurate picture of the system. With practice, anyone can master the skill of drawing a phase portrait by hand.
Gallery
Plot Phase Portrait With MATLAB And Simulink | Chengkun Li
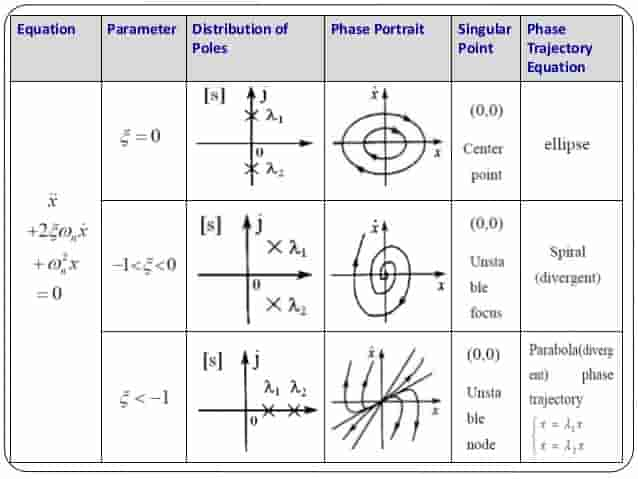
Photo Credit by: bing.com / matlab trajectory nonlinear simulink
Ordinary Differential Equations - Drawing A Phase Portrait Given
Photo Credit by: bing.com / phase differential portrait drawing eigenvectors given portraits ordinary paintingvalley
Real Analysis - Understanding How To Draw Phase Portraits/diagrams
Photo Credit by: bing.com /
ODE’s – MathGrapher
Photo Credit by: bing.com / orbits analytical
Sketching Phase Portraits - YouTube
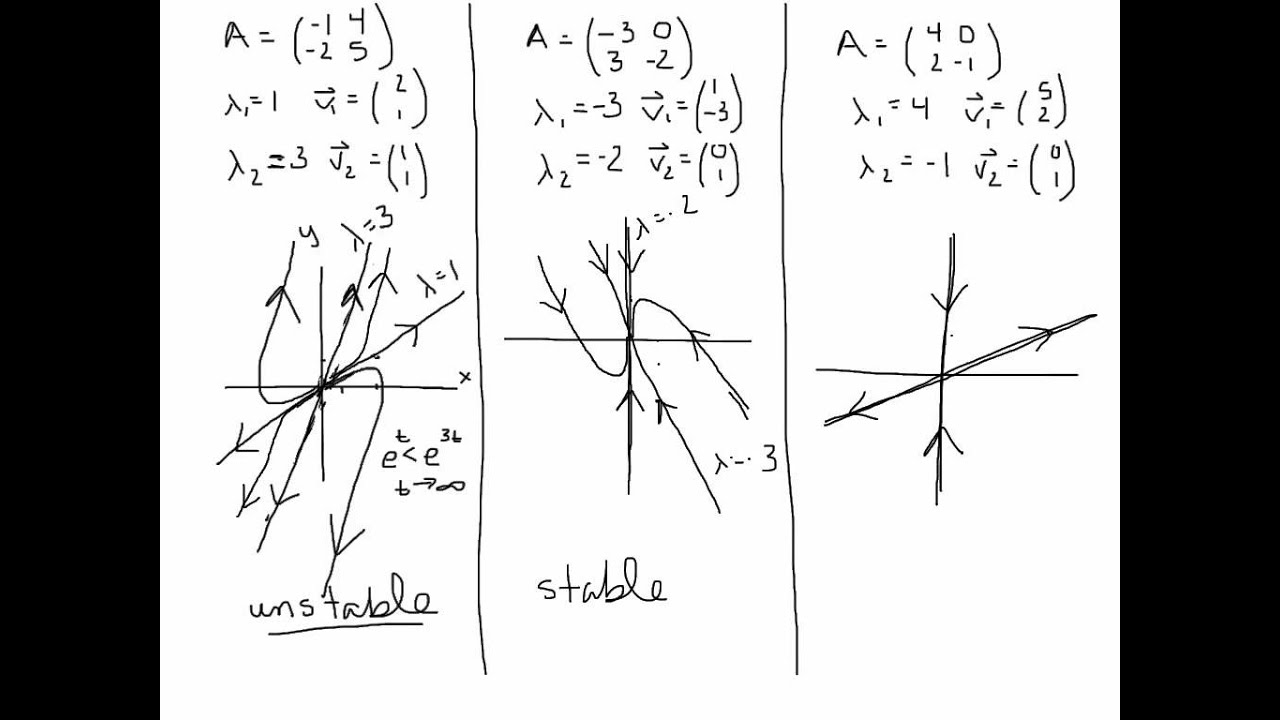
Photo Credit by: bing.com / phase portraits sketching
